Networked Multiagent Systems Lab

Research

Decentralized decision-making algorithms

In many multi-agent systems–stock market, teams of robots, devices in a microgrid–, agents in a network want to take actions that maximize their individual payoffs while their payoff values depend on the state of theenvironment and actions of the rest of the population. When agents have different and incomplete information about the state of the environment, agents are players in a game of incomplete information. I consider repeated play of this incomplete information game while agents acquire new information from their neighbors in the network and possibly from other sources after each time step. Acquiring this information alters agents’ beliefs leading to the selection of new actions which become known at the next play prompting further reevaluation of beliefs and corresponding actions. This research on networked multi-agent systems focuses on the interplay between understanding emerging behavior and designing optimal algorithms. It can be divided into two based on whether agents are rational or not.

The rational individual behavior in a game of incomplete information maximizes expected individual payoff given the rational actions of others. This rational behavior is called the Bayesian Nash equilibrium (BNE) solution concept. The determination of this BNE behavior involves forming Bayesian beliefs about the state and actions of other agents who have different beliefs about the state. We dub these games in which agents repeatedly make stage game rational decisions and acquire new information from their network as Bayesian Network games (BNG). In this context we talk of Bayesian learning because the agents’ goal can be reinterpreted as the eventual learning of peers’ actions so that expected payoffs coincide with actual payoffs. The question we try to answer in [Molavi et al 2015] is whether this information is eventually learned or not.

The burden of computing a BNE in repeated games is, in general, overwhelming even for small sized networks. This is an important drawback for the application of network games to the implementation of distributed actions in autonomous teams. Another purpose of this thrust is to develop algorithms to enable computation of rational actions. By focusing on quadratic payoff functions and initial Gaussian beliefs on the state, we derive the Quadratic Network Game (QNG) filter that agents can run locally to maximize their expected payoffs. The individual Bayesian belief forming process is akin to Kalman filter and involves a full network simulation by the individual [Eksin et al 2013, Eksin et al 2014].

A team of autonomous agents want to complete a task but each agent has different and incomplete information about the task. For instance, consider the problem of task assignment where a team of n robots wants to cover n targets. Each robot has a different belief on targets’ locations. The goal is to cover all targets by moving on to the target location while minimizing the total distance traversed. The communication limitations of each robot disallows aggregation of information on locations of targets. This problem is a potential game of incomplete information where there exists a state dependent global objective that agents affect through their individual actions.The optimal action profile maximizes this global objective for the realized environment’s state with the optimal action of an agent given by the corresponding action in the profile. The problem we address in this work is the determination of suitable actions when the probability distributions that agents have on the state of the environment are possibly different. These not entirely congruous beliefs result in mismatches between the action profiles that different agents deem to be optimal. As a consequence, when a given agent chooses an action to execute, it is important for it to reason about what the beliefs of other agents may be and what are the consequent actions that other agents may take. In this case, even though the interests of the members of the autonomous team are aligned, they have to resort to strategic reasoning and end up playing a game against uncertainty. The solutions that we propose to the problem above are variations of the fictitious play algorithm that take into account the distributed nature of the multi-agent system and the fact that the state of the environment is not perfectly known [Eksin & Ribeiro 2018, Swenson et al 2018, Aydin et al 2021, Aydin & Eksin 2022].

In the demonstrations below on the Robotarium, a team of mobile agents combine voluntary communication and communication-aware mobility protocols with decentralized fictitious play  to solve the target assignment problem [Aydin & Eksin 2021]:

  1. Team of 5 robots
  2. Team of 10 robots
  3. Team of 18 robots

 

Network optimization problems entail a group of agents with certain underlying connectivity that strive to minimize a global cost through appropriate selection of local variables. Optimal determination of local variables requires, in principle, global coordination of all agents. In ”’distributed”’ network optimization, agent coordination is further restricted to neighboring nodes. The optimization of the global objective is then achieved through iterative application of local optimization rules that update local variables based on information about the state of neighboring agents. Distributed network optimization is a common solution method for estimation and detection problems in wireless sensor networks (WSNs).

The goal of this project is to analyze emerging global behavior when agents are optimal in an average sense only. The expected optimality of an agent may stand for his resort to heuristic behavior, noisy communication with his neighbors or simply his lack of aptness to carry out the optimal action precisely. We define an agent’s aspiration to minimize his local cost function but failing to do it precisely as the ”’heuristic rational behavior”’ [Eksin & Ribeiro 2012].

The project on Bayesian Network Games started and evolved in collaboration with Pooya Molavi. We thank Ali Jadbabaie and Alejandro Ribeiro for their guidance and support. In the recent work on bounded rational algorithms, I was fortunate to collaborate with Brian Swenson and Soummya Kar. Special thanks goes to GritsLab, especially Magnus Egerstedt and Daniel Pickem for the open-access testbed Robotarium. At NetMas, Sarper Aydin (PhD candidate) has taken this research to exciting new directions in which we consider decentralized learning protocols for near-potential games and design of learning protocols given random communication networks. This research at NetMas is partially supported by NSF CCF 2008855.

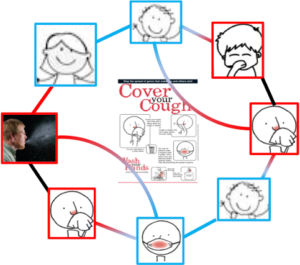Behavior Driven Epidemics on Networks

Epidemic diseases often spread via a form of contact among individuals. The existing web of interactions among the humans in a population determines the contact network over which the disease dynamics propagate. When a disease breaks out in the population, people that become aware of the disease can take precautionary measures to reduce their risk of getting infected. These measures are behavioral responses that depend on the local information of the individual on its risk of infection. In return, these responses affect the spread of the disease by changing the underlying contact rate among the individuals. In this project, we propose individual behavior response models to the disease prevalence in the population. We consider a model where individuals distance themselves from their local contacts based on their awareness. An individual forms its awareness based on information from its contacts in the social network. The efficacy of their distancing depends on the “amount of overlap” between their contagion network and their social network [Paarporn et al 2017]. We also consider a game theoretic basis for understanding the rational response of healthy and sick individuals over a network. The starting point for our model is the recognition that healthy individuals are concerned about contracting a disease from their sick contacts and may utilize protective measures. In addition, sick individuals may be concerned with spreading the disease to their healthy contacts and adopt preemptive measures [Eksin et al 2017]. Yet, in practice both protective and preemptive changes in behavior come with costs. We show using analytical derivations and simulations that the empathy of sick individuals is more important than the risk aversion of healthy individuals in eliminating the disease. More broadly, we hope that the current framework enables a deeper integration of game theory into studies of how behavior is shaped by and shapes disease dynamics. Overall, this research thrust points to potential pitfalls in current state-of-the-art disease forecasting models that neglect change of behavior during disease outbreaks, and to potential opportunities in local interventions.

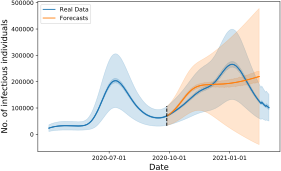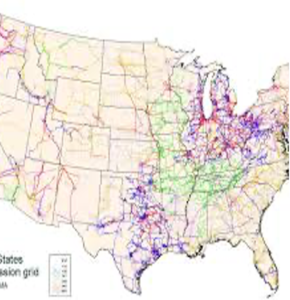
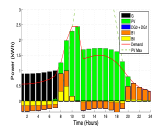
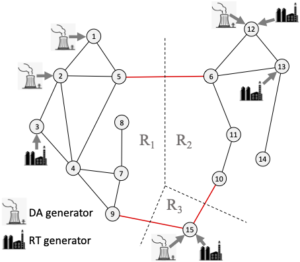Since COVID-19, this research thread has evolved to consider awareness and behavior driven models at the locality and individual levels showcasing the rich set of disease behaviors that can arise as a result [Khazaei et al 2021, Eksin et al 2021, Weitz et al 2020, Eksin et al 2019].

I am grateful to the invaluable support and help from Keith Paarporn (U of Colorado), Joshua Weitz (Georgia Tech) and Jeff Shamma (UIUC) in this thread. I also had the pleasure to work with wonderful collaborators such as J. Dushoff (McMaster), S.W. Park (Princeton), and M. Ndeffo-Mbah (A&M).

Decentralized energy systems and energy management

We are currently observing a multi-disciplinary research thrust to re-design the electricity grid. The overarching objective of this thrust is to have an efficient distribution system that is also robust. My research on this topic is primarily involved with the design of the communication among the entities of the grid — users, operators, suppliers — that will be supported by the adoption of smart meters and with the design for seamless integration of growing renewable energy generation into the grid.

 

In this project we consider the problem of matching power production to power consumption. This problem is exacerbated by the introduction of renewable sources, which, by their very nature, exhibit significant output fluctuations. This problem can be mitigated with the introduction of a system of smart meters.Smart meters control the power consumption of customers by managing the energy cycles of various devices while also enabling information exchanges between customers and the system operator as well as between customers themselves. The information flow and control abilities can be

combined with sophisticated pricing strategies so as to encourage a better match between power production and consumption. The effort of power providers to regulate the consumption of end users is referred to as demand response management. In our work, we study the rational consumer behavior in a repeated noncooperative game with incomplete information when the power provider employs an adaptive pricing policy. The adaptive price depends on renewable source output and total power consumption, and hence incentivizes customers with heterogeneous preferences to anticipate behavior of others and beware of their influence on price. Given the adaptive pricing strategy, we formulate the power consumption behavior of customers as a repeated noncooperative game with incomplete information. We provide an explicit characterization of unique Bayesian Nash equilibrium strategy when consumers only know their self-preference and the population preference distribution. Comparing the behavior of selfish consumers with the welfare maximizing consumers, selfish consumers tend to put more weight on their self-preference than on the mean population preference. The rational behavior is also characterized in a communication scheme where smart meters exchange consumption levels with neighboring meters. We use the QNG algorithm to compute equilibrium consumption and propagate beliefs. We observe that communication leads consumers to act similar to welfare maximizing individuals. In addition, communication is beneficial for welfare while having negligible effect on price and consumption levels. We further propose an ad-hoc pricing scheme that the operator can use to lower the peak-to-average ratio of total consumption by adjusting its target profit ratio [Eksin et al 2015, Eksin et al 2018].

 

At A&M this project evolved to consider intraday trading in electricity markets among system operators to increase reliability. In one work, we proposed an iterative mechanism for multiple areas to determine their terms of trading energy accounting for flow constraints. The iterative mechanism guaranteed convergence to a Nash equilibrium, a set of trading actions in which no area has unilateral profitable deviation. In such a solution some of the areas could lack the incentive to participate in the proposed mechanism as they may be worse off when they participate in the trading. Thus, we proposed a scheme for paying or charging participation fees, that creates an incentive compatible mechanism that is also budget balanced under certain technical restrictions [Garcia et al 2021]. A follow up study considers a similar iterative mechanism for improving intraday flexibility and reliability of areas [Khazaei et al 2022].

The project spun during my time at Boğaziçi University visiting Hakan Deliç’s lab. I thank Hakan Deliç for being a valuable and supportive collaborator in this project. At A&M, this project evolved in collaboration with Dr. Garcia, and grew with the support and hard work of our postdocs Roohallah Khatami and Hossein Khazaei, and PhD student Furkan Sezer.

At A&M, this project is partially supported by NSF Grants ECCS 1953694. CCF 2008855.